top of page
Decimals & Fractions

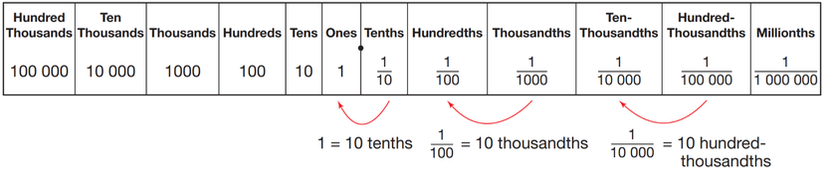
PLACE VALUE CHARTS
Place Values of Whole Numbers
Place Values of Decimals
Decimal: Shows numbers that are in-between numbers
1
2
In-Between Values: 1.2, 1.5, 1.7...
Place Value Chart:
Example 1) place 0.0139 on the place-value chart:
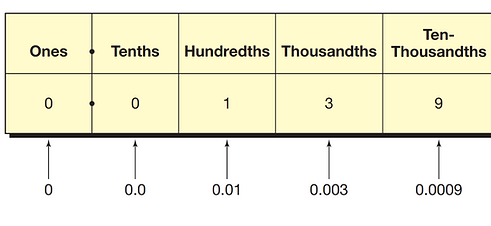
We can write this number in 2 forms:
Standard Form: 0.0139
Expanded Form: 0.01 + 0.003 + 0.0009
Practice
Practice PDFs available for download:

DECIMALS
Dividing Decimals
Example 1) Divide:
4.92 / 3
Step 1) How many times does "3" fit into 4?
3
4 9 2
1
-3
1
9

Step 2) Multiply "3" by step1 #
Step 3) Subtract the product
3
4 9 2
1
-3
1
9
6
-18
1
2
Step 4) Drop down the next number
Step 5) Repeat for each number, left to right

3
4 9 2
1
-3
1
9
6
-18
1
2
4
-12
0
1.64
Practice
Practice PDFs available for download:

FRACTIONS
Mixed & Improper Fractions

= 1 whole
= 1 whole
3
3
=
8
3
=

2
3
=
2
Improper Fractions: The numerator is greater than the denominator. Ex:
8
3
Mixed Fractions: has both a whole number and a fraction Ex:
Here, (2) is the whole number, and 2/3 is the fraction
2
3
2
Swapping Between Mixed & Improper Fractions
Mixed Number to Improper Fraction:
Step 1: Take your whole number (2) and multiply it by the denominator (3)
2
3
2
2 x 3
= 6

Step 2: Take that product (6) and add your numerator (2)
6 + 2 = 8

Step 3: Place you sum (8) as the numerator and keep (3) as the denominator
8
3
Improper Fraction to Mixed Number:
Step 1: Ask yourself how many times the denominator (3) fits into the numerator (8) without going over: That is your whole number part of the mixed number
8
3
3 fits into 8, 2 whole times

Step 2: Multiply the denominator (3) by the number you just found (2):
3 x 2 = 6

Step 3: Then take your numerator (8) and subtract the number you just found (6): this is you numerator for the
8 - 6 = 2

Step 4: Put it all together: (2) is the whole number outside the fraction.
(2) is the new numerator and (3) remains as the denominator.
2
3
2
Practice
Practice PDFs available for download:
Equivalent Ratios
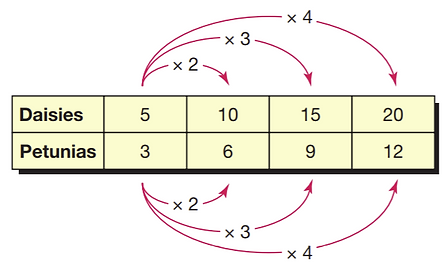
Equivalent Ratios: ratios of equal value
To find an equivalent ratio, you must always balance both numbers of the ratio
For example, to find an equivalent ratio of 5:3 we can multiply 5 by 2, and 3 by 2. This gives use 10:6.
10:6 is equivalent to 5:3 because we balanced both numbers of the term (multiplied both by 2)
Practice
Practice PDFs available for download:
Percents
Percents is another way to describe hundredths. Similar to fractions, it is a method to describe parts of a whole.
Here are 4 ways to describe the green part of the grid.
45 out of 100 squares are green
45
100
of the grid is green (Fraction)
0.45 of the grid is green (Decimal)
45% of the grid is green (Percent)
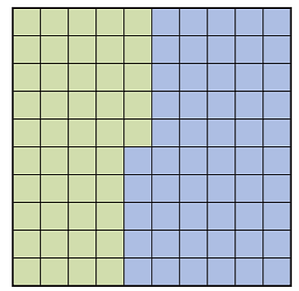
A percent is a special ratio comparing a number to 100.
45% means "45 out of 100"or "45 per hundred."
Practice
Practice PDFs available for download:
Multiplying Fractions
Example 1) Multiply:
7
x
3
4
Step 1) convert 7 to a fraction
7
1
x
3
4
Step 2) multiply across
7 x 3 = 21
1 x 4 = 4
Multiplying Mixed Numbers
Dividing Fractions
Strategy: Take the reciprocal (flipped) fraction, then multiply.
Example) Divide.
a)
7
4
÷
3
4
7
4
x
3
4
12
28
=
We can simplify by dividing both numerator and denominator by 4.
12
28
÷ 4
÷ 4
=
3
7
bottom of page
